深入理解计算机系统 Data Lab

发表于 更新于 阅读次数： 本文字数： 4k 阅读时长 ≈ 13 分钟

本文拷贝了 CSAPP 第一个实验 Data Lab 的题目和要求，并在尽可能避免直接透露答案的情况下记录自己解决问题时的思考片段。对于尚未正式开动但想提前小试牛刀的读者，可酌情食用。
本实验要求使用严格限制的 C 语言子集实现简单的逻辑、补码和浮点数函数，可以帮助 C 数据类型的位级表示和数据操作的位级行为。

说明

在开始解决问题前，务必仔细查看以下说明。你可能不经意间，会忽略了某些限制。

整数编码规则

将每个函数中的 return 语句替换为一行或多行实现该函数的 C 代码。代码必须符合以下样式：

1
2
3
4
5
6
7
8
9
10
11
int Funct(arg1, arg2, ...) {
    /* 简要说明实现的工作原理 */
    int var1 = Expr1;
    ...
    int varM = ExprM;

    varJ = ExprJ;
    ...
    varN = ExprN;
    return ExprR;
}

每个“Expr”都是仅使用以下内容的表达式：

  1. 整数常量 0 到 255（0xFF）。不得使用大常量，例如 0xffffffff。
  2. 函数参数和局部变量（无全局变量）。
  3. 一元整数运算 ! ~。
  4. ​​二元整数运算 & ^ | + << >>。

一些问题进一步限制了允许的运算符集（见函数的注释）。
每个“Expr”可能由多个运算符组成，不限于每行一个运算符。

明确禁止：

  1. 使用任何控制结构，例如 if、do、while、for、switch 等。
  2. 定义或使用任何宏。
  3. 在此文件中定义任何其他函数。
  4. 调用任何函数。
  5. 使用任何其他运算，例如 &&、||、- 或 ?:。
  6. 使用任何形式的转换。
  7. 使用除 int 之外的任何数据类型。这意味着不能使用数组、结构或联合。

“any form of casting”包括隐式类型转换吗？dlc 工具好像并不理会有符号数和无符号数运算时的隐式类型转换。

假设机器：

  1. 使用 32 位，补码表示整数。
  2. 执行算术右移。
  3. 如果移位量小于 0 或大于 31，则移位时的行为不可预测。

根据书中 P41 的旁注，C 语言标准规避了说明在位移量 k 大于等于组成数据类型所需的位数 w 时该如何做。尽管在许多机器上，实际位移量是通过计算 得到，但这种行为对于 C 程序来说是没有保证的。
实际上我也确实踩坑了，应该尽量保持位移量在合理范围内。

浮点数编码规则

对于需要实现浮点数运算的问题，编码规则不太严格。

  • 可以使用循环和条件控制。
  • 可以使用 int 和 unsigned。
  • 可以使用任意 int 和 unsigned 常量。
  • 可以对 int 和 unsigned 使用任何算术、逻辑或比较运算。

明确禁止：

  1. 定义或使用任何宏。
  2. 在此文件中定义任何其他函数。
  3. 调用任何函数。
  4. 使用任何形式的转换。
  5. 使用除 int 或 unsigned 之外的任何数据类型。这意味着不能使用数组、结构或联合。
  6. 使用任何浮点数据类型、运算或常量。

“使用浮点运算”是指什么？如果不能使用浮点数据类型，还有所谓“浮点运算”吗？

注意事项

  1. 使用 dlc（data lab checker，Steam 玩家？？？）编译器检查解决方案的合法性。
  2. 每个问题都有一个最大操作次数，限制可以在函数实现中使用整数、逻辑或比较运算的次数。dlc 会检查是否满足最大操作次数。注意，赋值操作 = 不计算在内，你可以随意使用，而不会受到惩罚。
  3. 使用 btest 测试工具检查函数是否正确。
  4. 使用 BDD 检查器正式验证函数。
  5. 每个函数的最大操作数在每个函数的注释中给出。

在下载的材料中并未找到 BDD，网上各种文章中也没有使用它。在课程官网给助教的说明中提到 BDD checker 已经使用多年。难道是并未对外提供？
之所以特别关注 BDD 是因为发现 btest 测试工具并不能充分检查函数的正确性，至少浮点数部分就有两道题目的测试用例没有覆盖所有分支情况。但仍然可以通过指定参数进行测试验证。

整数

bitXor

1
2
3
4
5
6
7
8
9
10
/* 
 * bitXor - x^y using only ~ and & 
 *   Example: bitXor(4, 5) = 1
 *   Legal ops: ~ &
 *   Max ops: 14
 *   Rating: 1
 */
int bitXor(int x, int y) {
    return 2;
}
  • 题目描述：仅使用 ~ 和 & 实现 x^y。
  • 允许的操作符：~ &
  • 最大操作次数：14
  • 评分：1

在掌握布尔代数运算的情况下，利用仅允许的两种操作符稍加试验，并不难得到解答。

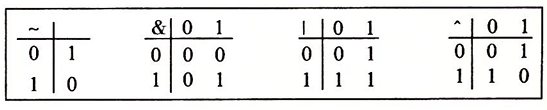
后来看到其他文章中都是通过德摩根定律推导公式，我ORZ。。。

tmin

1
2
3
4
5
6
7
8
9
/* 
 * tmin - return minimum two's complement integer 
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1
 */
int tmin(void) {
  return 2;
}
  • 题目描述：返回补码表示的整数的最小值。
  • 允许的操作符：! ~ & ^ | + << >>
  • 最大操作次数：4
  • 评分：1

在掌握整数的补码表示方法的同时，留意特殊值比如 、、 和 等等的位模式。

值 位模式
0x80000000
0x7fffffff
0x00000000
0xffffffff

注意：在解答整数部分的问题时，允许使用的常量范围为 0x00 到 0xFF，不能直接返回大常量 0x80000000。当然，后续会默认一些大常量是可以获得的。

通过移位运算用小常量构造大常量是非常实用的技巧。

isTmax

1
2
3
4
5
6
7
8
9
10
/*
 * isTmax - returns 1 if x is the maximum, two's complement number,
 *     and 0 otherwise 
 *   Legal ops: ! ~ & ^ | +
 *   Max ops: 10
 *   Rating: 1
 */
int isTmax(int x) {
  return 2;
}
  • 题目描述：判断是否为补码表示的整数的最大值，如果是则返回 1，否则返回 0。
  • 允许的操作符：! ~ & ^ | +
  • 最大操作次数：4
  • 评分：1

不仅可以通过移位运算用小常量构造大常量，还可以通过取反运算和溢出，实现特殊值 、、 和 之间的相互转换。

除了留意特殊值的位模式，还应留意它们可能具有一些独特的特性可以标识自己是自己。

不仅可以使用 == 判断两者是否相等，还可以通过异或运算的特性 判断两者是否相等，这是一个经典的技巧。

异或运算符 ^ 在 Latex 块中怎么都不能正确显示啊。

allOddBits

1
2
3
4
5
6
7
8
9
10
11
/* 
 * allOddBits - return 1 if all odd-numbered bits in word set to 1
 *   where bits are numbered from 0 (least significant) to 31 (most significant)
 *   Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 2
 */
int allOddBits(int x) {
  return 2;
}
  • 题目描述：判断是否全部奇数位都为 1，如果是则返回 1，否则返回 0。
  • 允许的操作符：! ~ & ^ | + << >>
  • 最大操作次数：12
  • 评分：2

最开始我看到评分提升了，还以为问题没那么简单，在未经测试的情况下想当然认为 allOddBits(0xAA) = 1。出门期间苦思冥想好久，感慨自己真聪明，发现功夫全白费了ORZ。

掩码（Mask）作为一串二进制数字，通过与目标的按位操作，达到屏蔽指定位的目的。

negate

1
2
3
4
5
6
7
8
9
10
/* 
 * negate - return -x 
 *   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2
 */
int negate(int x) {
  return 2;
}
  • 题目描述：返回相反数。
  • 允许的操作符：! ~ & ^ | + << >>
  • 最大操作次数：5
  • 评分：2

不使用 - 获得相反数是一个非常经典的技巧。推导过程也很有意思。

isAsciiDigit

1
2
3
4
5
6
7
8
9
10
11
12
/* 
 * isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
 *   Example: isAsciiDigit(0x35) = 1.
 *            isAsciiDigit(0x3a) = 0.
 *            isAsciiDigit(0x05) = 0.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 3
 */
int isAsciiDigit(int x) {
  return 2;
}
  • 题目描述：如果 x 的范围为 0x30 <= x <= 0x39，即字符 0 到 9 的 ASCII 编码，则返回 1。
  • 允许的操作符：! ~ & ^ | + << >>
  • 最大操作次数：15
  • 评分：3

从这题开始，有点卡。

回过头想，当时有点想当然，前面问题用到的小技巧让我以为解答都可以是“一蹴而就”和巧妙的，因而不甘心用“笨办法”，但这题恰恰是“一步一步走”。

通过 ! 将目标转换为 0 或 1。

后面使用 ! 时老感觉它在快速消耗操作次数。

注意，C 语言的位级运算和逻辑运算是不同的，一不留神容易犯错，但有时候它们刚好可以“李代桃僵”一下。

conditional

1
2
3
4
5
6
7
8
9
10
/* 
 * conditional - same as x ? y : z 
 *   Example: conditional(2,4,5) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 16
 *   Rating: 3
 */
int conditional(int x, int y, int z) {
  return 2;
}
  • 题目描述：实现和表达式 x ? y : z 相同的效果。
  • 允许的操作符：! ~ & ^ | + << >>
  • 最大操作次数：16
  • 评分：3

这题一开始就有思路，但实现时却卡了好一段时间。

注意到 * 和 & 的相似之处：

符号
* 1 0
& 0xffffffff 0x0

如何经过一个过程将非零转换为 0xffffffff，而零保持为 0x0 。

刚开始按常规思路使用移位运算和或运算，但是会超过最大操作次数。
感觉还是有点小巧妙呢！

isLessOrEqual

1
2
3
4
5
6
7
8
9
10
/* 
 * isLessOrEqual - if x <= y  then return 1, else return 0 
 *   Example: isLessOrEqual(4,5) = 1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3
 */
int isLessOrEqual(int x, int y) {
  return 2;
}
  • 题目描述：如果 x <= y，则返回 1，否则返回 0。
  • 允许的操作符：! ~ & ^ | + << >>
  • 最大操作次数：24
  • 评分：3

现在想来这题很简单，但是当时想其他题目想得头昏脑胀，感觉这题最让自己一头雾水。一方面是感觉 x 和 y 是对称的，运算也是对称的；另一方面是一时不知道如何将位级运算和目的关联起来；与此同时还被最大操作次数 24 恐吓住了。

有符号数。

logicalNeg

1
2
3
4
5
6
7
8
9
10
11
/* 
 * logicalNeg - implement the ! operator, using all of 
 *              the legal operators except !
 *   Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4 
 */
int logicalNeg(int x) {
  return 2;
}
  • 题目描述：使用除 ! 外所有允许使用的操作符，实现 ! 的效果。
  • 允许的操作符：~ & ^ | + << >>
  • 最大操作次数：12
  • 评分：4

卡了好久啊。
这道题目和 conditional 一样，从一开始我就有一个思路。注意到：

x x+1
0x0 0x1
0xffffffff 0x0

于是我就一门心思想着如何将非零转换为 0xffffffff，将零保持为 0x0。可是在不能使用 ! 的情况下，始终无法在最大操作次数之内实现。

换个角度，豁然开朗。不要被花里胡哨迷住了眼，有时候你只需要关注最低位。

howManyBits

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* howManyBits - return the minimum number of bits required to represent x in
 *             two's complement
 *  Examples: howManyBits(12) = 5
 *            howManyBits(298) = 10
 *            howManyBits(-5) = 4
 *            howManyBits(0)  = 1
 *            howManyBits(-1) = 1
 *            howManyBits(0x80000000) = 32
 *  Legal ops: ! ~ & ^ | + << >>
 *  Max ops: 90
 *  Rating: 4
 */
int howManyBits(int x) {
  return 0;
}
  • 题目描述：返回使用补码表示 x 所需的最小位数。
  • 允许的操作符：! ~ & ^ | + << >>
  • 最大操作次数：90
  • 评分：4

？

浮点数

在充分掌握浮点数编码之前，我不太喜欢浮点数，感觉它好麻烦好难；但在掌握之后，我感觉就编码部分而言信息量还好。
和网上的一些感受有点不同，我认为浮点数部分的问题比较直白。在条件限制不太严格的情况下，这些问题玩不出什么花来，按部就班地解决就好，不像前面的问题，会让人怀疑自己的智商。
当然，这并不代表以下问题可以很容易地解决，相反这些问题需要注意更多的细节和边界条件，因此耗时还是会很多。
与此同时，我确实感受到这些问题加深了我对浮点数编码的掌握程度。

掌握IEEE 浮点编码，浮点数的值被计算为

下列问题的花样离不开数字 2，而且我们会发现为了达到目的，无非是调整尾数（significand）或是阶码（exponent），同时留心非规格化、规格化以及特殊值等形式的边界条件。

有时候还需要回归朴素的二进制小数视角，认识到乘以 2 或是除以 2 就是在移动小数点。

注意，btest 测试工具不能充分验证函数实现的正确性，其测试用例集没有覆盖全部的分支情况（但仍可通过指定参数进行测试验证），因此需谨慎考虑自己的解决方案。

floatScale2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 
 * floatScale2 - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatScale2(unsigned uf) {
  return 2;
}
  • 题目描述：返回浮点数参数 f 的表达式 2*f 的相同位模式。其中参数和结果都以无符号整数传递，但它们将被解释为单精度浮点数的位级表示。当参数为 NaN 时，返回参数自身。
  • 允许的操作符：任何 int 和 unsigned 的操作符，包括 || && 以及 if while。
  • 最大操作次数：30
  • 评分：4

floatFloat2Int

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* 
 * floatFloat2Int - Return bit-level equivalent of expression (int) f
 *   for floating point argument f.
 *   Argument is passed as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point value.
 *   Anything out of range (including NaN and infinity) should return
 *   0x80000000u.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
int floatFloat2Int(unsigned uf) {
  return 2;
}
  • 题目描述：返回浮点数参数 f 的表达式 (int) f 的相同位模式。其中参数作为无符号整数传递，但它将被解释为单精度浮点数的位级表示。任何超出范围的值（包括 NaN 和无穷大）都应返回 0x80000000u。
  • 允许的操作符：任何 int 和 unsigned 的操作符，包括 || && 以及 if while。
  • 最大操作次数：30
  • 评分：4

个人认为这个问题相比于其他两个问题稍微困难一点，同时它对于帮助理解浮点数编码和二进制小数有很大帮助。

floatPower2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/* 
 * floatPower2 - Return bit-level equivalent of the expression 2.0^x
 *   (2.0 raised to the power x) for any 32-bit integer x.
 *
 *   The unsigned value that is returned should have the identical bit
 *   representation as the single-precision floating-point number 2.0^x.
 *   If the result is too small to be represented as a denorm, return
 *   0. If too large, return +INF.
 * 
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while 
 *   Max ops: 30 
 *   Rating: 4
 */
unsigned floatPower2(int x) {
    return 2;
}
  • 题目描述：对于任何 32 位整数 x，返回表达式 2.0^x 的相同位模式。如果结果太小而无法使用非规格化形式表示，则返回 0。如果太大，则返回 +INF。
  • 允许的操作符：任何 int 和 unsigned 的操作符，包括 || && 以及 if while。
  • 最大操作次数：30
  • 评分：4

总结和感想

有人说，Data Lab 是所有实验中最简单的一个。我不能完全认同。

在正式开始实验前，我自认为充分掌握了相关的知识，但实际过程并不顺利。说实话，确实有点打击人。这当然能说明理解知识并不完全等于掌握运用，但也不能说明我准备得不够到位，毕竟实验也是课程的一部分。
整数部分的坎坷，更多是对“奇淫巧计”（并非贬义）的不熟悉，思考的时候甚至会懊恼，感觉已经穷尽了变化，为什么得不到答案。而浮点数部分的顺利，算是对学习的“褒奖”。在后续完成 Bomb Lab 时也印证了自己的感受，Data Lab 不那么难，但不代表能有效推进解决；Bomb Lab 有难度，但在充分掌握的前提下，更有机会完成。

唉，大概也许可能真的是智商不够用了。