本文记录了常见的内存淘汰算法以及其中 LRU 和 LFU 的 Java 版本简单实现。
内存淘汰算法是操作系统和缓存系统中用来管理内存的一种方法。当内存空间不足时,新的数据需要加载进来,系统就会根据某种规则决定哪些数据应该被淘汰(从内存中移除)。不同的淘汰算法根据不同的策略来决定优先淘汰哪些数据,以提高内存的利用效率。
常见的内存淘汰算法
- 最近最少使用(LRU,Least Recently Used)
- 最不常用(LFU,Least Frequently Used)
- 先进先出(FIFO,First In First Out)
- 随机置换(Random Replacement)
- 最近最常使用(MRU,Most Recently Used)
- 时钟算法(Clock Algorithm)
- 有年龄的 LRU(Aging LRU)
- 最优置换算法(OPT,Optimal Page Replacement)
以上算法各有优劣,也许有人会认为在一定程度上 LFU 比 LRU 更“科学”一些。
- LRU 的科学性源自时间局部性,一个刚刚被使用到的数据很可能在不久的未来再次被使用。
- LFU 相比于 LRU 的改进之处在于它能更好地保存“热点数据”,即长期频繁访问的数据。但是常规的 LFU 也有其局限性,当一个缓存数据的访问频率在短期内发生急剧变化时,可能会产生“缓存污染”,导致热点数据被淘汰。
在 Redis 的内存淘汰 一文中,我们会看到 Redis 如何通过概率增加和定期衰减机制来减少 LFU 的缺点影响。
总之,在实际应用中,不同场景中的缓存数据可能具有不同的特点,因而适合不同的内存淘汰算法。(当然,更多时候缓存数据集可能平平无奇,直接分析缓存命中率可能更科学)
LRU 的简单实现
LRU 可以确保最近访问的数据被优先保留,而较久未访问的数据会被淘汰。LRU 的实现通常基于哈希表和双向链表,它们一起实现了 O(1) 时间复杂度的插入、删除和访问。
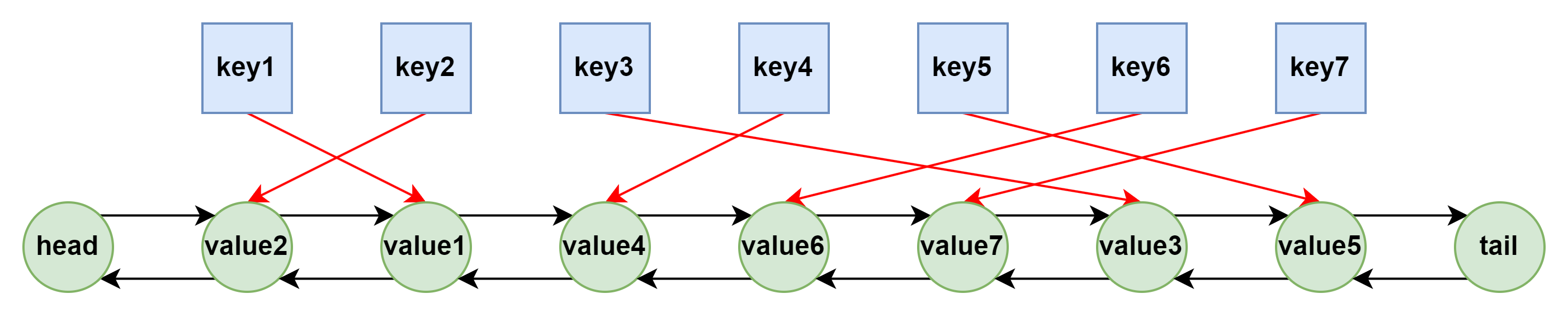
基于双向链表+哈希表
- 双向链表:用于按访问顺序保存缓存中的数据。链表头部表示最近使用的数据,尾部表示最久未被使用的数据。当缓存空间已满时,链表尾部的节点会被淘汰。
- 缓存项哈希表:用于记录键和双向链表节点的映射,以便 O(1) 时间复杂度查找缓存项。
以下是 LRUCache 的数据结构示意图:
以下是 Java 版本的 LRUCache 实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
| public class LRUCache {
private final int capacity;
private final Map<String, Node> cache;
private final Node head;
private final Node tail;
public LRUCache(int capacity) {
if (capacity <= 0) {
throw new IllegalArgumentException();
}
this.capacity = capacity;
cache = new HashMap<>();
head = new Node(null, 0);
tail = new Node(null, 0);
head.next = tail;
tail.prev = head;
}
public void put(String key, Integer value) {
if (cache.containsKey(key)) {
remove(cache.get(key));
}
Node node = new Node(key, value);
add(node);
cache.put(key, node);
if (cache.size() > capacity) {
Node lru = tail.prev;
remove(lru);
cache.remove(lru.key);
}
}
public Integer get(String key) {
if (cache.containsKey(key)) {
Node node = cache.get(key);
remove(node);
add(node);
return node.value;
}
return null;
}
private void add(Node node) {
node.next = head.next;
node.prev = head;
head.next.prev = node;
head.next = node;
}
private void remove(Node node) {
node.prev.next = node.next;
node.next.prev = node.prev;
node.next = null;
node.prev = null;
}
private static class Node {
private final String key;
private final Integer value;
private Node prev;
private Node next;
Node(String key, Integer value) {
this.key = key;
this.value = value;
}
}
}
|
LFU 的简单实现
LFU 可以确保最近常用的数据被优先保留,而最近不常用的数据会被淘汰。
基于哈希表+最小堆
一种方法是通过哈希表+最小堆实现。
- 缓存项哈希表:用于保存 key 到 Node 的映射,Node 包含 key、value 和 frequency。
- 最小堆:用于保存 Node,将 frequency 作为排序条件,以便淘汰最少使用的缓存项。
以下是 Java 版本的 LFUCache 实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| public class LFUCacheByMinHeap {
private final Map<String, Node> cache;
private final PriorityQueue<Node> minHeap;
private final int capacity;
public LFUCacheByMinHeap(int capacity) {
if (capacity <= 0) {
throw new IllegalArgumentException("illegal argument: capacity = " + capacity);
}
cache = new HashMap<>();
minHeap = new PriorityQueue<>(Comparator.comparingInt(a -> a.frequency));
this.capacity = capacity;
}
public void put(String key, Integer value) {
if (cache.containsKey(key)) {
Node node = cache.get(key);
minHeap.remove(node);
node.value = value;
node.frequency++;
minHeap.offer(node);
} else {
if (cache.size() >= capacity) {
Node lfu = minHeap.poll();
if (lfu != null) {
cache.remove(lfu.key);
}
}
Node node = new Node(key, value);
cache.put(key, node);
minHeap.offer(node);
}
}
public Integer get(String key) {
if (cache.containsKey(key)) {
Node node = cache.get(key);
minHeap.remove(node);
node.frequency++;
minHeap.offer(node);
return node.value;
}
return null;
}
private static class Node {
private final String key;
private Integer value;
private int frequency;
Node(String key, Integer value) {
this.key = key;
this.value = value;
frequency = 1;
}
}
}
|
考虑到取出使用频率最低的缓存项,想到使用最小堆是很自然的。最小堆执行 offer 和 poll 操作的时间复杂度为 O(log n),但实际上,由于更新最小堆中 Node 对象的 frequency 并不会自动引发最小堆的重新排序,需要先移除后添加,而移除任意节点操作的时间复杂度为 O(n)。不过,不论是 O(log n) 还是 O(n),对于缓存而言效率都很低。
基于双重哈希+双向链表
另一种方法是通过双重哈希+双向链表实现。
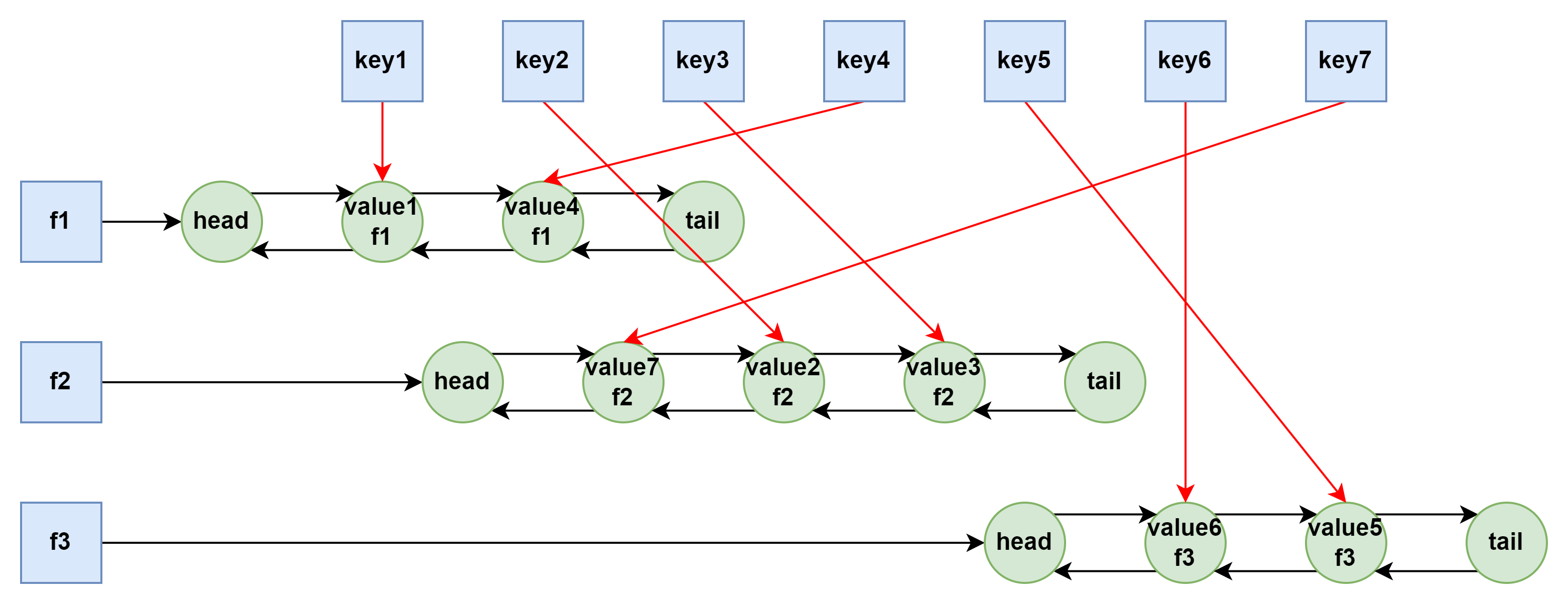
- 缓存项哈希表:用于保存 key 到 Node 的映射,Node 包含 key、value 和 frequency。
- 频率哈希表:用于保存 frequency 到一个双向链表的映射,链表存储所有使用频率相同的缓存项。
- 最小频率指针:用于保存当前缓存中最小的使用频率,以便快速找到需要淘汰的数据。
以下是 LFUCache 的数据结构示意图:
以下是 Java 版本的 LFUCache 实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
| public class LFUCache {
private final Map<String, Node> cache;
private final Map<Integer, DoubleLinkedList> frequencyMap;
private int minFrequency;
private final int capacity;
public LFUCache(int capacity) {
if (capacity <= 0) {
throw new IllegalArgumentException("illegal argument: capacity = " + capacity);
}
cache = new HashMap<>();
frequencyMap = new HashMap<>();
minFrequency = 0;
this.capacity = capacity;
}
public void put(String key, Integer value) {
if (cache.containsKey(key)) {
Node node = cache.get(key);
node.value = value;
updateFrequency(node);
} else {
if (cache.size() >= capacity) {
DoubleLinkedList l1 = frequencyMap.get(minFrequency);
Node lfu = l1.pop();
if (lfu != null) {
cache.remove(lfu.key);
}
}
Node node = new Node(key, value);
cache.put(key, node);
minFrequency = 1;
DoubleLinkedList l2 = frequencyMap.getOrDefault(1, new DoubleLinkedList());
l2.append(node);
frequencyMap.putIfAbsent(1, l2);
}
}
public Integer get(String key) {
if (cache.containsKey(key)) {
Node node = cache.get(key);
updateFrequency(node);
return node.value;
}
return null;
}
private void updateFrequency(Node node) {
int frequency = node.frequency;
DoubleLinkedList l1 = frequencyMap.get(frequency);
l1.remove(node);
if (l1.isEmpty()) {
frequencyMap.remove(frequency);
if (minFrequency == frequency) {
minFrequency++;
}
}
frequency = ++node.frequency;
DoubleLinkedList l2 = frequencyMap.getOrDefault(frequency, new DoubleLinkedList());
l2.append(node);
frequencyMap.putIfAbsent(frequency, l2);
}
private static class Node {
private final String key;
private Integer value;
private int frequency;
private Node prev;
private Node next;
Node(String key, Integer value) {
this.key = key;
this.value = value;
frequency = 1;
}
}
private static class DoubleLinkedList {
private final Node head;
private final Node tail;
DoubleLinkedList() {
head = new Node(null, 0);
tail = new Node(null, 0);
head.next = tail;
tail.prev = head;
}
void append(Node node) {
node.next = head.next;
node.prev = head;
head.next.prev = node;
head.next = node;
}
void remove(Node node) {
node.prev.next = node.next;
node.next.prev = node.prev;
node.prev = null;
node.next = null;
}
Node pop() {
if (isEmpty()) {
return null;
}
Node node = tail.prev;
remove(node);
return node;
}
boolean isEmpty() {
return head.next == tail;
}
}
}
|
和 LRU 的实现类似,关键点在于自定义双向链表和缓存项哈希表保存的是同一个节点对象,否则在链表上的查找操作的时间复杂度可能退化为 O(n)。